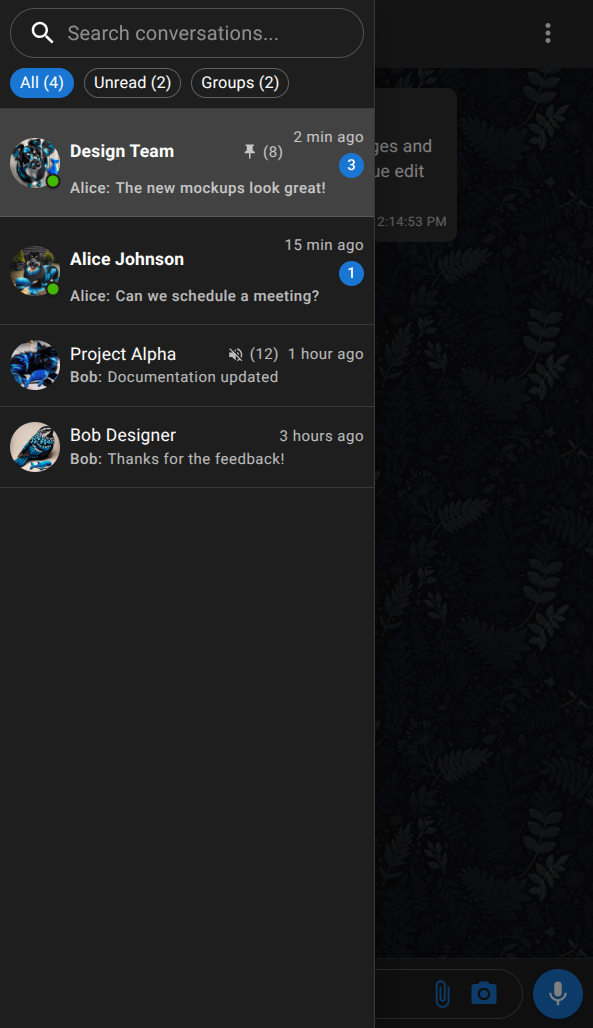
Why use Enkrypted Chat?
Explore below for more information on why Enkrypted Chat is secure and simple.

Be Yourself
Send and recieve text, voice messages, photos, videos, GIFs and much more using your device's data connection
Express Yourself
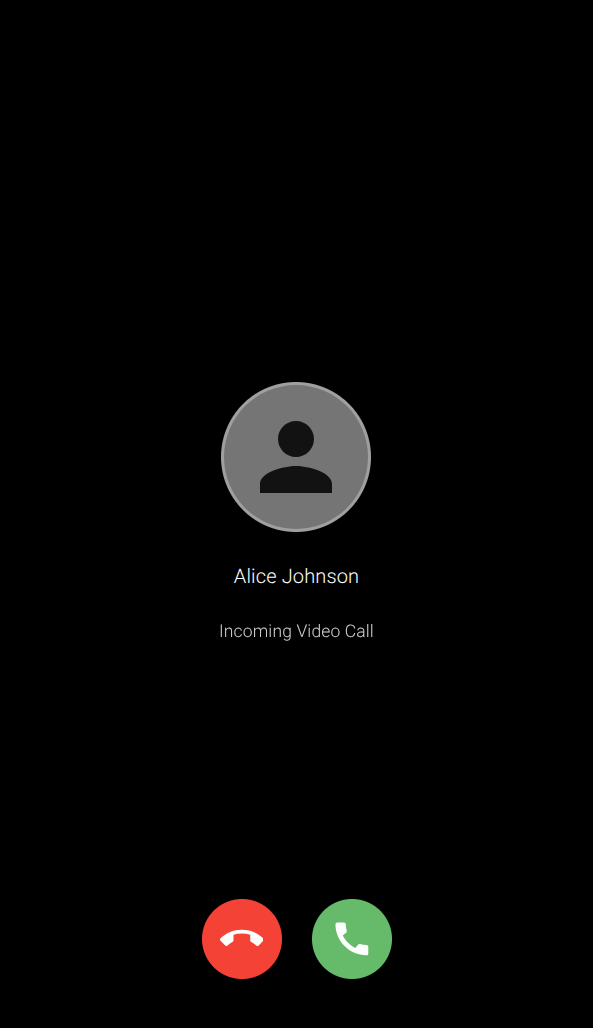
Send and recieve crystal clear voice and video calls with your friends and family.

Have Fun
Use emojis, stickers, and GIFs to express yourself and show your friends how you feel.
Share Securely
Advanced end-to-end encryption keeps your conversations secure. Only you and your peer can send/receive messages or have calls.
Signal Protocol
The Signal Protocol in rust that compiles to WASM for browser-based usage.
Post-Quantum Resistant Encryption
Using ML-KEM (Kyber) for a post-quantum resistant key encapsulation mechanism.

No Installation. No Registration. No Tracking. No Ads. No Limits.
You can use Enkrypted Chat without any real setup, so focus on the moments you want to share.

Research and Development
Innovating is a big part of what we do. We are always looking for new ways to improve the technology, user experience and the security of our products.

Sparcle
Experience Secure Messaging, Effortless File Sharing, and Crystal-clear Voice & Video Calls—all with cutting-edge P2P Technology.

Glitr.io
Using P2P E2EE file transfer, you have total privacy, seamless sharing. Connect Across all platforms. State-of-the-art encryption and universal file transfer.

P2P Chat
Experience Secure Messaging, Effortless File Sharing, and Crystal-clear Voice & Video Calls—all with cutting-edge P2P Technology.

Signal Protocol
The Signal Protocol in rust that compiles to WASM for browser-based usage.

Blog
Stay updated with our latest developments, technical insights, and security best practices. Deep dive into decentralized communication and privacy-focused technology.
- App Updates: Stay informed about the latest features and improvements in our apps.
- Research Insights: Discover the latest findings and innovations from our research team.
- Tutorials: Step-by-step guides to help you make the most of our apps and services.
- Project Details: In-depth information about our ongoing and upcoming projects.
Free For Everyone
positive-intentions is an independent project and is not funded or monetized in any way. We are not selling your data or using it for any purpose. Please consider supporting us with a donation.
Support Us